（本小题满分12分）已知函数
.
(1) 若
在
处取得极值, 求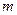
的值;
(2) 若以函数
图象上任意一点
为切点的切线的斜率
恒成立, 求正实数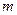的最小值;
(3) 在(1)的条件下, 若关于
的方程
在
上恰有两个不同的实根, 求实数
的取值范围.
相关试题
.
的解集;
对
恒成立,求实数a的取值范围.
.
；
的解集为
，求实数
的取值范围.
均为正实数，并且
，求证：
＜
，
＜
时，求
；
，命题
，若q是p的必要条件，求实数
的取值范围.
的函数
满足
,当
∈
时，
时，求
恒成立，求实数
的取值范围．推荐套卷
（本小题满分12分）已知函数.
(1) 若在处取得极值, 求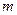的值;
(2) 若以函数图象上任意一点为切点的切线的斜率恒成立, 求正实数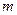的最小值;
(3) 在(1)的条件下, 若关于的方程在上恰有两个不同的实根, 求实数的取值范围.
粤公网安备 44130202000953号