某食品厂对生产的某种食品按行业标准分成五个不同等级,等级系数X依次为A,B,C,D,E.现从该种食品中随机抽取20件样品进行检验,对其等级系数进行统计分析,得到频率分布表如下:
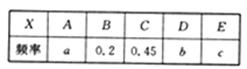
(1)在所抽取的20件样品中,等级系数为D的恰有3件,等级系数为E的恰有2件,求a,b,c的值;
(2)在(1)的条件下,将等级系数为D的3件样品记为x1,x2,x3,等级系数为E的2件样品记为y1,y2,现从x1,x2,x3,y1,y2这5件样品中一次性任取两件(假定每件样品被取出的可能性相同),试写出所有可能的结果,并求取出的两件样品是同一等级的概率.