（本小题满分12分）有3个不相同的球和4
个盒子,盒子的编号分别为1、2、3、4，将球逐个独立地、随机地放入4个盒子中去. 以
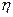表示其中至少有球的盒子的最小号码.(例如,事件
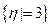表示第1号,第2号盒子都是空的, 第3号盒子中至少有一个球).
(1) 当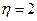
时, 求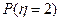
; (2) 求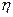的分布列及期望
.
上有一点
，以
为一个顶点，作抛物线的内接
，使得
所在直线的方程．
的顶点在原点，焦点在
轴上，斜率为
的直线交
两点，若
，且以
为直径的圆经过原点
，求直线
和抛物线
中，
，且
．求
，由此推出
表达式．
在
上至多有一实根．
：
及
：
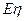的公共弦为直径的圆的方程．推荐套卷
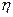（本小题满分12分）有3个不相同的球和4个盒子,盒子的编号分别为1、2、3、4，将球逐个独立地、随机地放入4个盒子中去. 以表示其中至少有球的盒子的最小号码.(例如,事件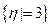表示第1号,第2号盒子都是空的, 第3号盒子中至少有一个球).
(1) 当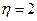时, 求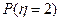; (2) 求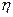的分布列及期望.
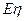粤公网安备 44130202000953号