（本小题满分13分）已知椭圆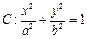
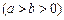的离心率为
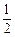，以原点为圆心，椭圆的短半轴为半径的圆与直线
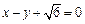相切．
（Ⅰ）求椭圆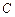
的方程；
（Ⅱ）设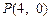
，
，
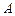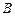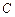是椭圆上关于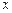
轴对称的任意两个不同的点，连结
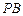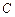交椭圆于另一点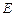
，证明直线
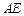与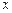轴相交于定点
．
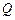S△ABC=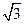
，求a的值．
的定义域；
的
的取值范围
则
的值？
与函数
的图像关于直线
对称．推荐套卷
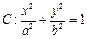
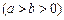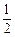（本小题满分13分）已知椭圆的离心率为，以原点为圆心，椭圆的短半轴为半径的圆与直线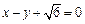相切．
（Ⅰ）求椭圆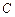的方程；
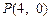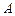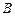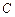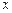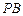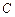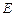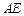（Ⅱ）设，，是椭圆上关于轴对称的任意两个不同的点，连结交椭圆于另一点，证明直线与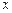轴相交于定点．
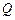S△ABC=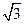，求a的值．
粤公网安备 44130202000953号