（
已知函数
（常数
）的图像过点
、
两点．
（1）求
的解析式；
（2）若函数
的图像与函数的图像关于直线
对称，若不等式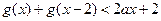
恒成立,求实数
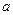的取值范围；
（3）若
是函数图像上的点列，
是
正半轴上的点列，
为坐标原点，
是一系列正三角形，记它们的边长是
，探求数列
的通项公式，并说明理由．
相关试题
，则
”的逆命题，否命题，逆否命题
在坐标轴上，离心率为
，且过点（4，-
）
的面积。
有两个不等的负根，q:方程
无实根，若p或q为真，p且q为假，求m的取值范围。
定圆
动圆M与定圆
都外切，求动圆圆心M的轨迹方程。推荐套卷
（
已知函数（常数）的图像过点、两点．
（1）求的解析式；
（2）若函数的图像与函数的图像关于直线对称，若不等式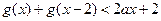恒成立,求实数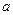的取值范围；
（3）若是函数图像上的点列，是正半轴上的点列，为坐标原点，是一系列正三角形，记它们的边长是，探求数列的通项公式，并说明理由．
粤公网安备 44130202000953号