设函数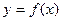 的定义域为全体R,当x<0时,
的定义域为全体R,当x<0时, ,且对任意的实数x,y∈R,有
,且对任意的实数x,y∈R,有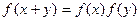 成立,数列
成立,数列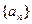 满足
满足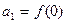 ,且
,且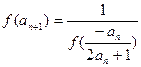 (n∈N*)
(n∈N*)
(Ⅰ)求证: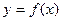 是R上的减函数;
是R上的减函数;
(Ⅱ)求数列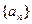 的通项公式;
的通项公式;
(Ⅲ)若不等式 对一切n∈N*均成立,求k的最大值.
对一切n∈N*均成立,求k的最大值.
推荐套卷
设函数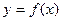 的定义域为全体R,当x<0时,
的定义域为全体R,当x<0时, ,且对任意的实数x,y∈R,有
,且对任意的实数x,y∈R,有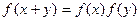 成立,数列
成立,数列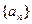 满足
满足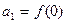 ,且
,且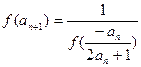 (n∈N*)
(n∈N*)
(Ⅰ)求证: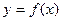 是R上的减函数;
是R上的减函数;
(Ⅱ)求数列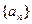 的通项公式;
的通项公式;
(Ⅲ)若不等式 对一切n∈N*均成立,求k的最大值.
对一切n∈N*均成立,求k的最大值.