(此题平行班做)(本小题满分12分)
某班主任对全班50名学生的学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:

(Ⅰ)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是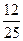 ,请完成上面的
,请完成上面的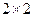 列联表;
列联表;
 |
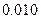 |
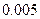 |
 |
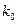 |
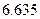 |
 |
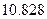 |
(Ⅱ)在(1)的条件下,试运用独立性检验的思想方法分析:在犯错误概率不超过0.1%的情况下判断学生的学习积极性与对待班级工作的态度是否有关?并说明理由.
推荐套卷
(此题平行班做)(本小题满分12分)
某班主任对全班50名学生的学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:

(Ⅰ)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是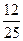 ,请完成上面的
,请完成上面的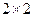 列联表;
列联表;
 |
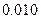 |
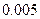 |
 |
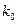 |
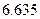 |
 |
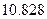 |
(Ⅱ)在(1)的条件下,试运用独立性检验的思想方法分析:在犯错误概率不超过0.1%的情况下判断学生的学习积极性与对待班级工作的态度是否有关?并说明理由.