（本小题满分13分）
袋中有大小相同的三个球，编号分别为1、2和3，从袋中每次取出一个球，若取到的球的编号为偶数，则把该球编号加1（如：取到球的编号为2，改为3）后放回袋中继续取球；若取到球的编号为奇数，则取球停止，用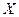
表示所有被取球的编号之和．
（Ⅰ）求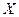的概率分布；
（Ⅱ）求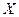的数学期望与方差．
＝
．
的值；
是R上的奇函数，且当
时，
在区间[1,3]上有最大值5和最小值2，求
的值
|
或
}，B＝{
或
}，若
，求实数
的取值范围．
，
，求
的值推荐套卷
（本小题满分13分）
袋中有大小相同的三个球，编号分别为1、2和3，从袋中每次取出一个球，若取到的球的编号为偶数，则把该球编号加1（如：取到球的编号为2，改为3）后放回袋中继续取球；若取到球的编号为奇数，则取球停止，用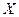表示所有被取球的编号之和．
（Ⅰ）求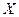的概率分布；
（Ⅱ）求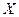的数学期望与方差．
粤公网安备 44130202000953号