（本小题满分12分）
若
，则
，
，
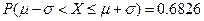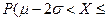
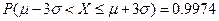．在2010年黄冈中学理科实验班招生考试中，有5000人参加考试，考生的数学成绩服
．
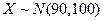（Ⅰ）在5000名考生中，数学分数在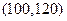
之间的考生约有多少人；
（Ⅱ）若对数学分数从高到低的前114名考生予以录取，问录取分数线为多少？
相关试题
中，
分别是角
的对边，且
．
的大小；
，求
、
满足关系式
．
；
中,d=2,n=15,
求
及
求
中，
是数列
项和，对任意
，有
的值；
，求数列
的前
。
推荐套卷
（本小题满分12分）
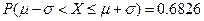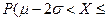
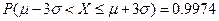若，则，，．在2010年黄冈中学理科实验班招生考试中，有5000人参加考试，考生的数学成绩服．
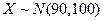（Ⅰ）在5000名考生中，数学分数在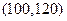之间的考生约有多少人；
（Ⅱ）若对数学分数从高到低的前114名考生予以录取，问录取分数线为多少？
粤公网安备 44130202000953号