((本题15分)
已知直线l的方程为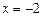 ,且直线l与x轴交点
,且直线l与x轴交点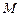 ,圆
,圆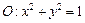 与x轴交
与x轴交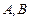 两点.
两点.
(1)过M点的直线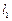 交圆于
交圆于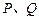 两点,且圆孤
两点,且圆孤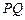 恰为圆周的
恰为圆周的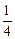 ,求直线
,求直线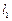 的方程;
的方程;
(2)求以l为准线,中心在原点,且与圆O恰有两个公共点的椭圆方程;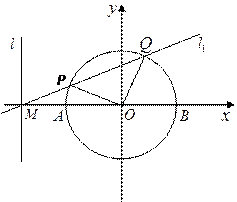 (3)过M点作直线
(3)过M点作直线 与圆相切于点
与圆相切于点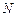 ,设(2)中椭圆的两个焦点分别为
,设(2)中椭圆的两个焦点分别为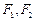 ,求三角形
,求三角形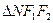 面积.
面积.
推荐套卷
((本题15分)
已知直线l的方程为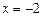 ,且直线l与x轴交点
,且直线l与x轴交点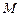 ,圆
,圆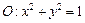 与x轴交
与x轴交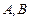 两点.
两点.
(1)过M点的直线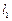 交圆于
交圆于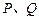 两点,且圆孤
两点,且圆孤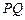 恰为圆周的
恰为圆周的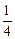 ,求直线
,求直线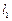 的方程;
的方程;
(2)求以l为准线,中心在原点,且与圆O恰有两个公共点的椭圆方程;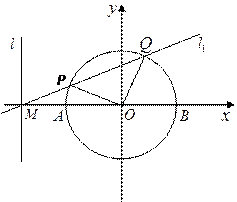 (3)过M点作直线
(3)过M点作直线 与圆相切于点
与圆相切于点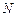 ,设(2)中椭圆的两个焦点分别为
,设(2)中椭圆的两个焦点分别为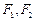 ,求三角形
,求三角形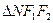 面积.
面积.