（本小题满分12分）四川灾后重建工程督导评估小组五名专家被随机分配到A、B、C、D四所不同的学校进行重建评估工作，要求每所学校至少有一名专家。
（1）求评估小组中甲、乙两名专家同时被分配到A校的概率；
（2）求评估小组中甲、乙两名专家不在同一所学校的概率；
（3）设随机变量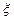
为这五名专家到A校评估的人数，求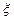的数学期望E。
相关试题
，
．
时，求函数
的最小值；
恒成立，试求实数
的取值范围．
中，
分别为
的对边,已知
．
；
，
时，求
是递增的等差数列，
，求数列
的前n项和
．
，
，
．
的单调递增区间；
时，对任意
，不等式
恒成立，求实数的
取值范围．
的奇函数
．
；
，总有
，求实数
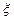的取值范围．推荐套卷
（本小题满分12分）四川灾后重建工程督导评估小组五名专家被随机分配到A、B、C、D四所不同的学校进行重建评估工作，要求每所学校至少有一名专家。
（1）求评估小组中甲、乙两名专家同时被分配到A校的概率；
（2）求评估小组中甲、乙两名专家不在同一所学校的概率；
（3）设随机变量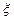为这五名专家到A校评估的人数，求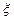的数学期望E。
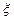粤公网安备 44130202000953号