(本题满分14分)设有抛物线C：
，通过原点O作C的切线
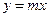，使切点P在第一象限.
（1）求m的值，以及P的坐标；
（2）过点P作切线的垂线，求它与抛物线的另一个交点Q；
（3）设C上有一点R，其横坐标为
，为使DOPQ的面积小于DPQR的面积，试求的取值范围.
相关试题
，函数
.
，求函数
的极值与单调区间；
处的切线与直线
平行，求
的值；
有三个公共点，求
，
，且
.
时，求
;
，求函数
的最值及相应的
的值.
的前
项和为
，且满足
，
满足
，求数列
．
的周期为
，其中
．
的值及函数
的单调递增区间；
中，设内角A、B、C所对边的长分别为a、b、c，若
，
，f(A)=
，求b的值．
的前
项和为
，已知
，
是
和
的等比中项.相关知识点
推荐套卷
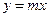(本题满分14分)设有抛物线C：，通过原点O作C的切线，使切点P在第一象限.
（1）求m的值，以及P的坐标；
（2）过点P作切线的垂线，求它与抛物线的另一个交点Q；
（3）设C上有一点R，其横坐标为，为使DOPQ的面积小于DPQR的面积，试求的取值范围.
粤公网安备 44130202000953号