某食品
厂进行蘑菇的深加工，每公斤蘑菇的成本20元，并且每公斤蘑菇的加工费为
元（为常数，且
，设该食品厂每公斤蘑菇的出厂价为
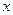元（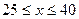
），根据市场调查，销售量
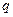与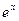
成反比，当每公斤蘑菇的出厂价为30元时，日销售量为100公斤.
（Ⅰ）求该工厂的每日利润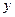
元与每公斤蘑菇的出厂价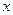元的函数关系式；
（Ⅱ）若
，当每公斤蘑菇的出厂价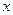为多少元时，该工厂的利润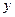最大，并求最大值.
相关试题
“若
则二次方程
没有实根”.
的否命题； (2)判断命题
在一个周期内的图象如下图所示。
，且方程
有两个不同的实数根，求实数m的取值范围和这两个根的和。
推荐套卷
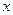某食品厂进行蘑菇的深加工，每公斤蘑菇的成本20元，并且每公斤蘑菇的加工费为元（为常数，且，设该食品厂每公斤蘑菇的出厂价为元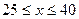（），根据市场调查，销售量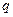与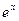成反比，当每公斤蘑菇的出厂价为30元时，日销售量为100公斤.
（Ⅰ）求该工厂的每日利润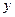元与每公斤蘑菇的出厂价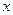元的函数关系式；
（Ⅱ）若，当每公斤蘑菇的出厂价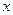为多少元时，该工厂的利润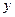最大，并求最大值.
粤公网安备 44130202000953号