(本小题满分12分)
已知抛物线 (
( )的焦点为椭圆
)的焦点为椭圆 的右焦点,点
的右焦点,点 、
、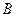 为抛物线上的两点,
为抛物线上的两点,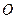 是抛物线的顶点,
是抛物线的顶点,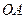 ⊥
⊥ .
.
(Ⅰ)求抛物线的标准方程;
(Ⅱ)求证:直线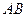 过定点
过定点 ;
;
(Ⅲ)设弦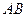 的中点为
的中点为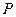 ,求点
,求点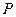 到直线
到直线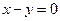 的距离的最小值.
的距离的最小值.
推荐套卷
(本小题满分12分)
已知抛物线 (
( )的焦点为椭圆
)的焦点为椭圆 的右焦点,点
的右焦点,点 、
、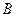 为抛物线上的两点,
为抛物线上的两点,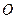 是抛物线的顶点,
是抛物线的顶点,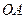 ⊥
⊥ .
.
(Ⅰ)求抛物线的标准方程;
(Ⅱ)求证:直线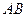 过定点
过定点 ;
;
(Ⅲ)设弦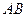 的中点为
的中点为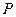 ,求点
,求点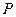 到直线
到直线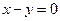 的距离的最小值.
的距离的最小值.