(满分20分)本题有2小题,第1小题12分,第2小题8分.
设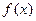 为定义域为
为定义域为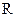 的函数,对任意
的函数,对任意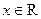 ,都满足:
,都满足: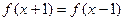 ,
,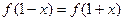 ,且当
,且当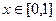 时,
时,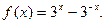
(1)请指出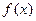 在区间
在区间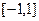 上的奇偶性、单调区间、最大(小)值和零点,并运用相关定义证明你关于单调区间的结论;
上的奇偶性、单调区间、最大(小)值和零点,并运用相关定义证明你关于单调区间的结论;
(2)试证明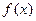 是周期函数,并求其在区间
是周期函数,并求其在区间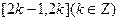 上的解析式.
上的解析式.
推荐套卷
(满分20分)本题有2小题,第1小题12分,第2小题8分.
设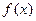 为定义域为
为定义域为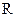 的函数,对任意
的函数,对任意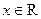 ,都满足:
,都满足: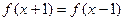 ,
,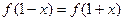 ,且当
,且当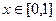 时,
时,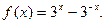
(1)请指出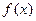 在区间
在区间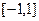 上的奇偶性、单调区间、最大(小)值和零点,并运用相关定义证明你关于单调区间的结论;
上的奇偶性、单调区间、最大(小)值和零点,并运用相关定义证明你关于单调区间的结论;
(2)试证明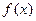 是周期函数,并求其在区间
是周期函数,并求其在区间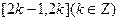 上的解析式.
上的解析式.