本题有⑴、⑵、⑶三个选考题,每题7分,请考生任选两题作答,满分14分,如果多做,则按所做的前两题计分.
(1)(本小题满分7分)选修4—2:矩阵与变换
已知二阶矩阵M有特征值 及对应的一个特征向量
及对应的一个特征向量 ,并且矩阵M对应的变换将点
,并且矩阵M对应的变换将点 变换成
变换成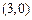 ,求矩阵M。
,求矩阵M。
(2)(本小题满分7分)选修4—4:坐标系与参数方程
过点M(3,4),倾斜角为 的直线
的直线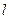 与圆C:
与圆C: (
( 为参数)相交于A、B两点,试确定
为参数)相交于A、B两点,试确定 的值。
的值。
(3)(本小题满分7分)选修4—5:不等式选讲
已知实数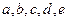 满足
满足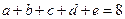 ,
, ,试确定
,试确定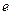 的最大值。
的最大值。
相关知识点
推荐套卷
 ,
,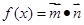 +
+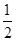 (1)若
(1)若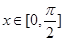 ,f(x)=
,f(x)=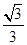 ,求
,求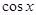 的值; (2)在△ABC中,角A,B,C的对边分别是
的值; (2)在△ABC中,角A,B,C的对边分别是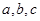 ,且满足
,且满足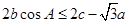 ,求f(B)的取值范围.
,求f(B)的取值范围. .(
.( 为常数)
为常数) 时,①求
时,①求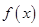 的单调增区间;②试比较
的单调增区间;②试比较 与
与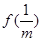 的大小;
的大小; ,若对任意给定的
,若对任意给定的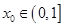 ,在
,在 上总存在两个不同的
上总存在两个不同的 ,使得
,使得 成立,求
成立,求 的右焦点为
的右焦点为 ,离心率
,离心率 ,
,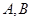 是椭圆上的两动点,动点
是椭圆上的两动点,动点 满足
满足 (其中实数
(其中实数 为常数).
为常数). ,且直线
,且直线 过
过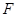 点且垂直于
点且垂直于 轴时,求过
轴时,求过 三点的外接圆方程;
三点的外接圆方程; 与
与 的斜率乘积
的斜率乘积 ,问是否存在常数
,问是否存在常数 ,其中
,其中 ,若存在求出
,若存在求出
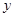 (单位:千克)与销售价格
(单位:千克)与销售价格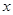 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式 ,其中
,其中 ,
,  为常数,已知销售价格为5元/千克时,每日可售出该商品11千克.
为常数,已知销售价格为5元/千克时,每日可售出该商品11千克.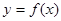 的最小值等于4,且
的最小值等于4,且 .
. 的解析式;
的解析式; ,求
,求 ,
,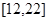 ,求
,求 的值.
的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号