(本小题满分13分)
我校要用三辆汽车把高二文科学生从学校送到古田参加社会实践活动,已知学校到古田有两条公路,汽车走公路①堵车的概率为 ,不堵车的概率为
,不堵车的概率为 ;汽车走公路②堵车的概率为
;汽车走公路②堵车的概率为 ,不堵车的概率为
,不堵车的概率为 .若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响
.若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响
(I)若三辆汽车中恰有一辆汽车被堵的概率为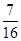 ,求汽
,求汽 车走公路②堵车的概率P。
车走公路②堵车的概率P。
(II)在(1)的条件下,求三辆汽车中被堵车辆的个数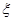 的分布列和数学期望。
的分布列和数学期望。
推荐套卷
(本小题满分13分)
我校要用三辆汽车把高二文科学生从学校送到古田参加社会实践活动,已知学校到古田有两条公路,汽车走公路①堵车的概率为 ,不堵车的概率为
,不堵车的概率为 ;汽车走公路②堵车的概率为
;汽车走公路②堵车的概率为 ,不堵车的概率为
,不堵车的概率为 .若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响
.若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响
(I)若三辆汽车中恰有一辆汽车被堵的概率为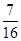 ,求汽
,求汽 车走公路②堵车的概率P。
车走公路②堵车的概率P。
(II)在(1)的条件下,求三辆汽车中被堵车辆的个数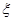 的分布列和数学期望。
的分布列和数学期望。