甲有一只放有a本《周易》,b本《万年历》,c本《吴从纪要》的书箱,且a+b+c ="6" (a,b,c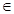 N),乙也有一只放有3本《周易》,2本《万年历》,1《吴从纪要》的书箱,两人各自从自己的箱子中任取一本书(由于每本书厚薄、大小相近,每本书被抽取出的可能性一样),规定:当两本书同名时甲将被派出去完成某项任务,否则乙去.
N),乙也有一只放有3本《周易》,2本《万年历》,1《吴从纪要》的书箱,两人各自从自己的箱子中任取一本书(由于每本书厚薄、大小相近,每本书被抽取出的可能性一样),规定:当两本书同名时甲将被派出去完成某项任务,否则乙去.
(1) 用a、b、c表示甲去的概率;
(2) 若又规定:当甲取《周易》,《万年历》,《吴从纪要》而去的得分分别为1分、2分、3分,否则得0分,求甲得分的期望的最大值及此时a、b、c的值.