(本小题满分12分)
已知直线 与椭圆
与椭圆 交于两点
交于两点 ,椭圆上的点到下焦点距离的最大值、最小值分别为
,椭圆上的点到下焦点距离的最大值、最小值分别为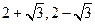 ,向量
,向量 ,O为坐标原点。
,O为坐标原点。 (Ⅰ)求椭圆的方程;
(Ⅰ)求椭圆的方程;
(Ⅱ)判断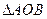 的面积是否为定值,如果是,请给予证明;如果不是,请说明理由。
的面积是否为定值,如果是,请给予证明;如果不是,请说明理由。
推荐套卷
(本小题满分12分)
已知直线 与椭圆
与椭圆 交于两点
交于两点 ,椭圆上的点到下焦点距离的最大值、最小值分别为
,椭圆上的点到下焦点距离的最大值、最小值分别为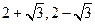 ,向量
,向量 ,O为坐标原点。
,O为坐标原点。 (Ⅰ)求椭圆的方程;
(Ⅰ)求椭圆的方程;
(Ⅱ)判断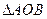 的面积是否为定值,如果是,请给予证明;如果不是,请说明理由。
的面积是否为定值,如果是,请给予证明;如果不是,请说明理由。