已知M(-3,0)﹑N(3,0),P为坐标平面上的动点，且直线PM与直线PN的斜率之积为常数m(m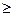
-1,m
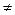0).
(1)求P点的轨迹方程并讨论轨迹是什么曲线？
(2)若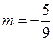
, P点的轨迹为曲线C,过点Q(2,0)斜率为
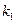的直线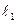
与曲线C交于不同的两点A﹑B,AB中点为R,直线OR(O为坐标原点)的斜率为
，求证
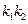为定值；
（3）在（2）的条件下，设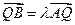
，且
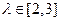，求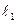在y轴上的截距的变化范围.
相关试题
,其中
.
时，求不等式
的解集；
的解集为
，求
的值.
，AF＝3，求FG的长．推荐套卷
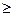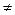已知M(-3,0)﹑N(3,0),P为坐标平面上的动点，且直线PM与直线PN的斜率之积为常数m(m-1,m0).
(1)求P点的轨迹方程并讨论轨迹是什么曲线？
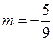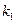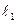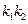(2)若, P点的轨迹为曲线C,过点Q(2,0)斜率为的直线与曲线C交于不同的两点A﹑B,AB中点为R,直线OR(O为坐标原点)的斜率为，求证为定值；
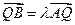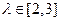（3）在（2）的条件下，设，且，求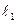在y轴上的截距的变化范围.
粤公网安备 44130202000953号