已知抛物线C: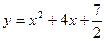
, 过抛物线C上点M且与M处的切线垂直的直线称为抛物线C在点M的法线。
⑴若抛物线C在点M的法线的斜率为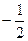 
，求点M的坐标
；
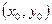⑵设P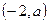
为C对称轴上的一点，在C上是否存在点，使得C在该点的法线通过点P。若有，求出这些点，以及C在这些点的法线方程；若没有，请说明理由。
相关试题
的长方体被截面
所截而得到的，其中
．
；
到平面
中，
，底面
是直角梯形，
是直角，
，求异面直线
与
所成角的大小．
中，
，
面
，
，求面
与面
所成二面角的正切值．
的棱长为2，
分别是
上的动点，且
，确定
．
中，底面是等腰直角三角形，
，侧棱
分别是
与
的中点，点
在平面
上的射影是
的重心
，求点
到平面
的距离．
相关知识点
推荐套卷
已知抛物线C: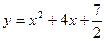, 过抛物线C上点M且与M处的切线垂直的直线称为抛物线C在点M的法线。
⑴若抛物线C在点M的法线的斜率为 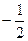，求点M的坐标；
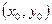⑵设P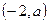为C对称轴上的一点，在C上是否存在点，使得C在该点的法线通过点P。若有，求出这些点，以及C在这些点的法线方程；若没有，请说明理由。
粤公网安备 44130202000953号