每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):
按类用分层抽样的方法在这个月生产的 轿车中抽取50辆,其中有A类轿车10辆
轿车中抽取50辆,其中有A类轿车10辆 .
.
(Ⅰ)求z的值.
(Ⅱ)用分层抽样的方法在C类轿车中抽取一个容量为5的样本.将 该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
| |
轿车A |
轿车B |
轿 车C 车C |
| 舒适型 |
100 |
150 |
z |
| 标准型 |
300 |
450 |
600 |
推荐套卷
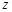 是复数,
是复数, 与
与 均为实数,且复数
均为实数,且复数 在复平面上对应的点在第一象限,求实数
在复平面上对应的点在第一象限,求实数 的取值范围.
的取值范围. 为坐标原点,已知向量
为坐标原点,已知向量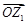 ,
,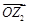 分别对应复数
分别对应复数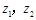 ,且
,且 ,
, ,
,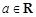 .若
.若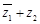 可以与任意实数比较大小,求
可以与任意实数比较大小,求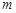 为何值时,复数
为何值时,复数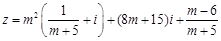 .
. 对应的点落在射线
对应的点落在射线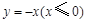 上,
上,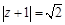 ,求复数
,求复数 .
.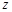 是虚数
是虚数 是实数,且
是实数,且 .
. 的值及
的值及 ,求证:
,求证: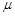 为纯虚数;
为纯虚数; 的最小值.
的最小值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号