（本小题满分12分）
已知A、B、C是直线l上的三点，O是直线l外一点，向量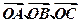
满足
＝[f(x
)＋2f′(1)]
－ln(x＋1)
。
（Ⅰ）求函数y＝f(x)的表达式； （Ⅱ）若x>0，证明：f(x)> 
；
（Ⅲ）若不等式
x2≤f(x2)＋m2－2m－3对x∈[－1,1]恒成立，求实数m的取值范围。
相关试题
。
：
；（2）至少有一个实数
，使得
。
：
，
；（2）
：所有的正方形都是矩形；
：对一切
，都有
，若
为真，求实数
的取值范围。
的定义域是
，且满足
,
,如果对于
,都有
,（1）求
；（2）解不等式
。推荐套卷
（本小题满分12分）
已知A、B、C是直线l上的三点，O是直线l外一点，向量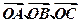满足＝[f(x)＋2f′(1)]－ln(x＋1)。
（Ⅰ）求函数y＝f(x)的表达式； （Ⅱ）若x>0，证明：f(x)> ；
（Ⅲ）若不等式x2≤f(x2)＋m2－2m－3对x∈[－1,1]恒成立，求实数m的取值范围。
粤公网安备 44130202000953号