(本小题满分12分)
已知函数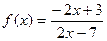 ,若存在实数
,若存在实数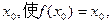 则称
则称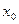 是函数
是函数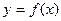 的一个不动点.
的一个不动点.
(I)证明:函数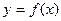 有两个不动点;
有两个不动点;
(II)已知a、b是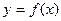 的两个不动点,且
的两个不动点,且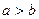 .当
.当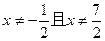 时,比较
时,比较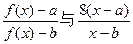 的大小;
的大小;
(III)在数列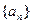 中,
中,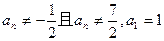 ,等式
,等式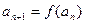 对任何正整数n都成立,求数列
对任何正整数n都成立,求数列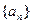 的通项公式.
的通项公式.
推荐套卷
(本小题满分12分)
已知函数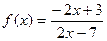 ,若存在实数
,若存在实数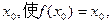 则称
则称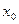 是函数
是函数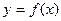 的一个不动点.
的一个不动点.
(I)证明:函数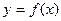 有两个不动点;
有两个不动点;
(II)已知a、b是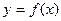 的两个不动点,且
的两个不动点,且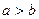 .当
.当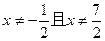 时,比较
时,比较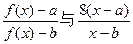 的大小;
的大小;
(III)在数列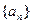 中,
中,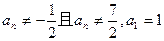 ,等式
,等式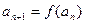 对任何正整数n都成立,求数列
对任何正整数n都成立,求数列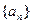 的通项公式.
的通项公式.