已知点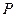 为圆
为圆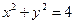 上的动点,且
上的动点,且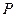 不在
不在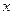 轴上,
轴上,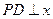 轴,垂足为
轴,垂足为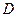 ,线段
,线段 中点
中点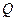 的轨迹为曲线
的轨迹为曲线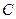 ,过定点
,过定点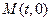
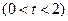 任作一条与
任作一条与 轴不垂直的直线
轴不垂直的直线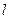 ,它与曲线
,它与曲线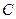 交于
交于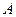 、
、 两点。
两点。
(1)求曲线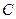 的方程;
的方程;
(2)试证明:在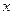 轴上存在定点
轴上存在定点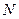 ,使得
,使得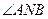 总能被
总能被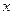 轴平分。
轴平分。
推荐套卷
已知点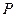 为圆
为圆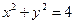 上的动点,且
上的动点,且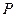 不在
不在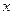 轴上,
轴上,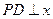 轴,垂足为
轴,垂足为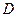 ,线段
,线段 中点
中点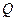 的轨迹为曲线
的轨迹为曲线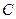 ,过定点
,过定点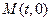
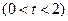 任作一条与
任作一条与 轴不垂直的直线
轴不垂直的直线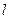 ,它与曲线
,它与曲线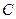 交于
交于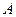 、
、 两点。
两点。
(1)求曲线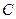 的方程;
的方程;
(2)试证明:在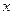 轴上存在定点
轴上存在定点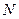 ,使得
,使得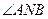 总能被
总能被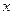 轴平分。
轴平分。