（本小题满分16分）
某校学生社团心理学研究小组在对学生上课注意力集中情况的调查研究中，发现其在
40分钟的一节课中，注意力指数p与听课时间t（单位：分钟）之间的关系满足如图
所示的曲线．当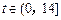
时
，曲线是二次函数图象的一部分，当
时，曲线
是函数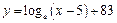
(
，
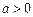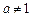)图象的一部分．根据专家研究，当注意力指数p大于80时学习效果最佳．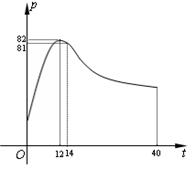
（1）试求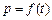
的函数关系式；
（2）教师在什么时段内安排核
心内容，能使得学生学习效果最佳？请说明理由．
相关试题
的展开式中各项系数和为64．
；
，且
为实数，求z．
的最大值；
，使
成立，试求
的取值范围；
且
时，不等式
恒成立，求
.
的奇偶性；
；
，
，求
，
的值.推荐套卷
（本小题满分16分）
某校学生社团心理学研究小组在对学生上课注意力集中情况的调查研究中，发现其在
40分钟的一节课中，注意力指数p与听课时间t（单位：分钟）之间的关系满足如图
所示的曲线．当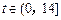时，曲线是二次函数图象的一部分，当时，曲线
是函数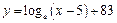(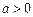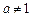，)图象的一部分．根据专家研究，当注意力指数p大于80时学习效果最佳．
（1）试求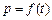的函数关系式；
（2）教师在什么时段内安排核心内容，能使得学生学习效果最佳？请说明理由．
粤公网安备 44130202000953号