已知抛物线y=ax2+bx+c经过A(-4,3)、B(2,0)两点,当x=3和x=-3时,这条抛物线上对应点的纵坐标相等.经过点C(0,-2)的直线l与 x轴平行,O为坐标原点.
(1)求直线AB和这条抛物线的解析式;
(2)以A为圆心,AO为半径的圆记为⊙A,判断直线l与⊙A的位置关系,并说明理由;
(3)设直线AB上的点D的横坐标为-1,P(m,n)是抛物线y=ax2+bx+c上的动点,当△PDO的周长最小时,求四边形CODP的面积.
相关知识点
推荐套卷
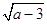 +
+ +5,求此等腰三角形的周长.
+5,求此等腰三角形的周长.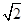 是无理数,而无理数是无限不循环小数.因此,
是无理数,而无理数是无限不循环小数.因此, =x+y,其中x是整数,且0<y<1,求x-y的值.
=x+y,其中x是整数,且0<y<1,求x-y的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号