如图，在矩形ABCD中，AB=m（m是大于0的常数），BC=8，E为线段BC上的动点（不与B、C重合）．连结DE，作EF⊥DE，EF与射线BA交于点F，设CE=x，BF=y．
（1）求y关于x的函数关系式；
（2）若m=8，求x为何值时，y的值最大，最大值是多少？
（3）若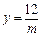
，要使△DEF为等腰三角形，m的值应为多少？
时，分别求代数式①
②
的值.
②
的值.
的值.
cm，
cm时，阴影部分的面积.相关知识点
推荐套卷
如图，在矩形ABCD中，AB=m（m是大于0的常数），BC=8，E为线段BC上的动点（不与B、C重合）．连结DE，作EF⊥DE，EF与射线BA交于点F，设CE=x，BF=y．
（1）求y关于x的函数关系式；
（2）若m=8，求x为何值时，y的值最大，最大值是多少？
（3）若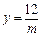，要使△DEF为等腰三角形，m的值应为多少？
粤公网安备 44130202000953号