(本小题10分)选修4—1:几何证明选讲
如图,设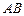 为⊙O的任一条不与直线l垂直的直径,
为⊙O的任一条不与直线l垂直的直径,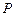 是⊙O与l的公共点,
是⊙O与l的公共点,
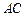 ⊥l,
⊥l,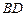 ⊥l,垂足分别为
⊥l,垂足分别为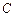 ,
, ,且
,且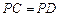 ,
,

求证:
(I)l是⊙O的切线;
(II)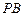 平分∠ABD.
平分∠ABD.
推荐套卷
(本小题10分)选修4—1:几何证明选讲
如图,设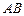 为⊙O的任一条不与直线l垂直的直径,
为⊙O的任一条不与直线l垂直的直径,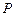 是⊙O与l的公共点,
是⊙O与l的公共点,
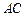 ⊥l,
⊥l,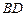 ⊥l,垂足分别为
⊥l,垂足分别为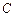 ,
, ,且
,且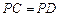 ,
,

求证:
(I)l是⊙O的切线;
(II)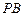 平分∠ABD.
平分∠ABD.