某学校为了解600名初中毕业生体育考试成绩的情况(满分30分,得分为整数),从中随机抽取了部分学生的体育考试成绩,制成如下图所示的频数分布直方图.已知成绩在15.5~18.5这一组的频率为,请回答下列问题:
(1)在这个问题中,总体是_____________________,样本容量是________;
(2)请补全成绩在21.5~24.5这一组的频数分布直方图;
(3)如果成绩在18分以上的为“合格”,请估计该校初中毕业生中体育成绩为“合格”的人数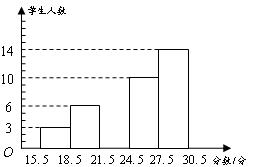
相关知识点
推荐套卷

 //BC,交直线CD于点F.将直线
//BC,交直线CD于点F.将直线 (t
(t 0),直角梯形ABCD被直线
0),直角梯形ABCD被直线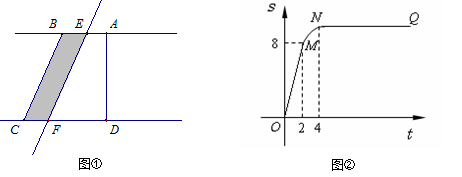
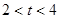 时,求S关于
时,求S关于 内接于⊙
内接于⊙ ,过点
,过点 作直线
作直线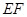 ,
, 为非直径的弦,且
为非直径的弦,且 ,BC=2,连接OC并延长交EF于点M,求由弧BC、线段BM和CM所围成的图形的面积.
,BC=2,连接OC并延长交EF于点M,求由弧BC、线段BM和CM所围成的图形的面积.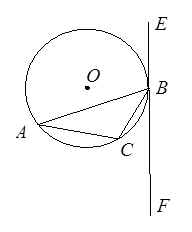
 粤公网安备 44130202000953号
粤公网安备 44130202000953号