（本小题共16
分）
已知数列
各项均不为0，其前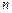
项和为
，且对任意
都有
（
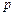为大于1的常数），记f（n）
．
（1）求
；
（2）试比较
与
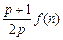的大小（）；
（3）求证：（2n-1）f（n）≤f（1）+f（2）+…+f（2n-1） ≤[1-（）2n-1] （n∈N*）
相关试题
，求数列{bn}的前n项和Sn.
＜－1，且它们的前n项和Sn有最大值，求使得Sn＜0的n的最小值．推荐套卷
（本小题共16分）
已知数列各项均不为0，其前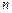项和为，且对任意都有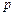（为大于1的常数），记f（n）．
（1）求；
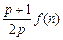（2）试比较与的大小（）；
（3）求证：（2n-1）f（n）≤f（1）+f（2）+…+f（2n-1） ≤[1-（）2n-1] （n∈N*）
粤公网安备 44130202000953号