已知点 和互不相同的点
和互不相同的点 ,
,
满足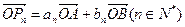 ,其中
,其中 分别为等差数列和等比数列,O为坐标原点,若
分别为等差数列和等比数列,O为坐标原点,若 为线段AB的中点。
为线段AB的中点。
(1)求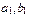 的值;
的值;
(2)证明 的公差为d =0,或
的公差为d =0,或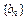 的公比为q=1,点
的公比为q=1,点 在同一直线上;
在同一直线上;
(3)若d  0,且q
0,且q  1,点
1,点 能否在同一直线上?证明你的结论
能否在同一直线上?证明你的结论
推荐套卷
已知点 和互不相同的点
和互不相同的点 ,
,
满足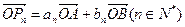 ,其中
,其中 分别为等差数列和等比数列,O为坐标原点,若
分别为等差数列和等比数列,O为坐标原点,若 为线段AB的中点。
为线段AB的中点。
(1)求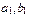 的值;
的值;
(2)证明 的公差为d =0,或
的公差为d =0,或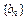 的公比为q=1,点
的公比为q=1,点 在同一直线上;
在同一直线上;
(3)若d  0,且q
0,且q  1,点
1,点 能否在同一直线上?证明你的结论
能否在同一直线上?证明你的结论