(本题满分10分)
在一个口袋中有n个小球,其中2个是白球,其余为红球,这些球除颜色外,其余都相同,在看不到球的条件下,从袋中随机地取出一个球,它是红球的概率是.
(1)求n的值;
(2)甲、乙、丙三人玩一个游戏:把这n个球分别标号为1,2,3,…n,三人按先后顺序各摸出一个球(不放回),哪个摸出一号球,哪个获胜.(若不分胜负,再重新摸)请你用画树形图的方法分析:他们各自获胜的机会与他们摸球的顺序是否有关?若有关,请指出第几个摸球更有利;若无关,请说明理由
相关知识点
推荐套卷
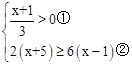 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.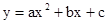 与x轴正半轴交于A、B两点,与y轴交于点C,直线
与x轴正半轴交于A、B两点,与y轴交于点C,直线 经过A、C两点,且AB=2.
经过A、C两点,且AB=2.
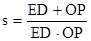 ,当t为何值时,s有最小值,并求出最小值。
,当t为何值时,s有最小值,并求出最小值。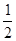

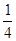


 粤公网安备 44130202000953号
粤公网安备 44130202000953号