（本小题满分12分）
如图，正方形ADEF和等腰梯形ABCD垂直，已知BC=2AD=4，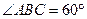
，
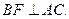
（I）求证：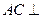
面ABF；
（II）求异面直线BE与AC所成的角的余弦值；
（III）在线段BE上是否存在一点P，使得平面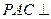
平面BCEF？若存在，求出
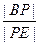的值，若不存在，请说明理由。
相关试题
是偶函数
，若函数f(x)与g(x)的图像有且只有一个公共点，求实数a的取值范围。
为减函数，
对
恒成立，求实数m的取值范围.
的一条对称轴为
，且
为第四象限角，其终边上一个点为
，且
，求
的值
、
，使
，
.
的轨迹
的方程；
上任取一点
做曲线
、
，求证：直线
恒过一定点.
推荐套卷
（本小题满分12分）
如图，正方形ADEF和等腰梯形ABCD垂直，已知BC=2AD=4，，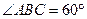
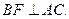
（I）求证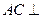：面ABF；
（II）求异面直线BE与AC所成的角的余弦值；
（III）在线段BE上是否存在一点P，使得平面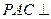平面BCEF？若存在，求出 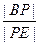的值，若不存在，请说明理由。
粤公网安备 44130202000953号