（本小题满分12分）
某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器的垂直弹射高度：在C处进行该仪器的垂直弹射，观测点A、B两地相距100米，
，在A地听到弹射声音的时间比B地晚
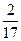秒，A地测得该仪器在C处时的俯角为15°A地测得最高点H时的仰角为30°，求该仪器的垂直弹射高度CH（声音的传播速度为340米/秒）
相关试题
的圆柱，求圆柱的表面积.
都有
并且当 
时，
, 
0,求函数f(x)=log2
的最大值和最小值。(14分)
[-3,2]，求f(x)=
的最小值与最大值。推荐套卷
（本小题满分12分）
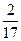某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器的垂直弹射高度：在C处进行该仪器的垂直弹射，观测点A、B两地相距100米，，在A地听到弹射声音的时间比B地晚秒，A地测得该仪器在C处时的俯角为15°A地测得最高点H时的仰角为30°，求该仪器的垂直弹射高度CH（声音的传播速度为340米/秒）
粤公网安备 44130202000953号