设MN是双曲线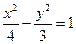
的弦，且MN与
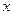轴垂直，
、
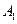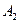是双曲线的左、右顶点．
（Ⅰ）求直线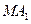
和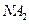
的交点的轨迹C的方程；
（Ⅱ）
设直线y=x－1与轨迹C交于A、B两点，若轨迹C上的点P满足
(
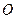为坐标原点，
，
)
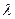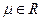求证：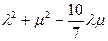
为定值,并求出这个定值．
的解析式； 
（
）在区间
上减函数，求实数
的取值范围？
的定义域；
成立的
的取值范围。
,满足
，求实数
的取值范围
,求函数
的零点；
相关知识点
推荐套卷
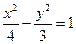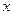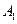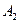设MN是双曲线的弦，且MN与轴垂直，、是双曲线的左、右顶点．
（Ⅰ）求直线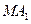和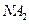的交点的轨迹C的方程；
（Ⅱ）设直线y=x－1与轨迹C交于A、B两点，若轨迹C上的点P满足( 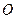为坐标原点，，)
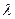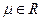求证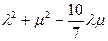：为定值,并求出这个定值．
粤公网安备 44130202000953号