据气象中心观察和预测:发生于M地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t(h)的函数图象如图所示,过线段OC上一点T(t,0)作 横轴的垂线l,梯形OABC在直线l左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km).
横轴的垂线l,梯形OABC在直线l左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km).
(1)当t=4时,求s的值;
(2)将s随t变化的规律用数学关系式表示出来;
(3)若N城位于M地正南方向,且距M地650 km,试判断这场沙尘暴是否会侵袭到N城,如果会,在沙尘暴发生后多长时间它将侵袭到N城?如果不会,请说明理由.
相关知识点
推荐套卷
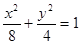 有相同的焦点,实半轴长为
有相同的焦点,实半轴长为 .
. 的方程;
的方程;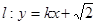 与双曲线
与双曲线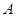 和
和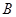 ,且
,且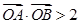 (其中
(其中 为原点),求
为原点),求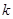 的取值范围.
的取值范围. 在
在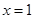 及
及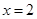 时取得极值.
时取得极值. 的值;
的值;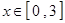 ,都有
,都有 成立.求
成立.求 的取值范围.
的取值范围. 过点
过点 ,且在点
,且在点 处与直线
处与直线 相切,求
相切,求 的值.
的值. 与抛物线
与抛物线 交于
交于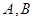 两点,求证:
两点,求证: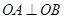 .
. 共渐近线,且过点
共渐近线,且过点 的双曲线的标准方程.
的双曲线的标准方程. 粤公网安备 44130202000953号
粤公网安备 44130202000953号