(本小题满分14分)如图1,在直角梯形ABCP中,AP//BC,AP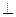 AB,AB=BC=
AB,AB=BC=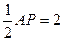 ,D是AP的中点,E,F,G分别 为PC、PD、CB的中点,将
,D是AP的中点,E,F,G分别 为PC、PD、CB的中点,将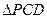 沿CD折起,使得
沿CD折起,使得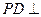 平面ABCD, 如图2.
平面ABCD, 如图2.
(Ⅰ)求三棱椎D-PAB的体积;
(Ⅱ) 求证:AP//平面EFG;
(Ⅲ)求二面角G—EF-D的大小。

推荐套卷
(本小题满分14分)如图1,在直角梯形ABCP中,AP//BC,AP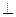 AB,AB=BC=
AB,AB=BC=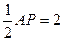 ,D是AP的中点,E,F,G分别 为PC、PD、CB的中点,将
,D是AP的中点,E,F,G分别 为PC、PD、CB的中点,将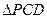 沿CD折起,使得
沿CD折起,使得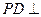 平面ABCD, 如图2.
平面ABCD, 如图2.
(Ⅰ)求三棱椎D-PAB的体积;
(Ⅱ) 求证:AP//平面EFG;
(Ⅲ)求二面角G—EF-D的大小。
