(本小题满分12分)
如图，已知空间四边形ABCD中，BC=AC,
AD=BD,E是AB的中点，
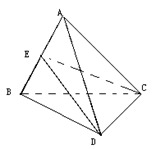
求证：
AB⊥平面CDE；
平面CDE⊥平面ABC;
若G为△ADC的重心，试在线段AB上确定一点F，使得GF∥平面CDE.
相关试题
ABC中，
内角A、B、C的对边分别为
，已知
且
的值； （2）设
，求a+c的值
分别表示三个内角A、B、C的对边，
，且
，
=7，求角C
，若
，求
的值
，
，求ac＋bd的最大值．
相关知识点
推荐套卷
(本小题满分12分)
如图，已知空间四边形ABCD中，BC=AC,AD=BD,E是AB的中点，
求证：
AB⊥平面CDE；
平面CDE⊥平面ABC;
若G为△ADC的重心，试在线段AB上确定一点F，使得GF∥平面CDE.
粤公网安备 44130202000953号