(本小题满分12分)
已知F1、F2分别是双曲线x2-y2=1的两个焦点,O为坐标原点,圆O是以F1F2为直径的圆,直线l:y=kx+b (b>0)与圆O相切,并与双曲线相交于A、B两点.
(1)根据条件求出b和k满足的关系式;
(2)向量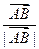 在向量
在向量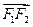 方向的投影是p,当(×)p2=1时,求直线l的方程;
方向的投影是p,当(×)p2=1时,求直线l的方程;
(3)当(× )p2=m且满足2≤m≤4时,求DAOB面积的取值范围.
)p2=m且满足2≤m≤4时,求DAOB面积的取值范围.
相关知识点
推荐套卷
(本小题满分12分)
已知F1、F2分别是双曲线x2-y2=1的两个焦点,O为坐标原点,圆O是以F1F2为直径的圆,直线l:y=kx+b (b>0)与圆O相切,并与双曲线相交于A、B两点.
(1)根据条件求出b和k满足的关系式;
(2)向量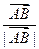 在向量
在向量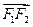 方向的投影是p,当(×)p2=1时,求直线l的方程;
方向的投影是p,当(×)p2=1时,求直线l的方程;
(3)当(× )p2=m且满足2≤m≤4时,求DAOB面积的取值范围.
)p2=m且满足2≤m≤4时,求DAOB面积的取值范围.