（本小题满分14分）设函数f(x) =" x2" + bln(x+1),
（1）若对定义域的任意x，都有f(x)≥f(1)成立，求实数b的值；
（2）若函数f(x)在定义域上是单调函数，求实数b的取值范围；
（3）若b = -1,，证明对任意的正整数n，不等式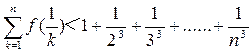
都成立
相关试题
为实数，函数
.K]
，求
2)求
的最小值； 
，直接写出(不需给出演算步骤)不等式
的解集.
，当
时，有
，解关于x的不等式
是R上的偶函数,且当
时,函数的解析式为
的值;
时,函数的解析式;
上是减函数;
的终边上有一点P（
，m），且
m，求
与
的值
的集合；
的图象经过怎样的变化而得到的相关知识点
推荐套卷
（本小题满分14分）设函数f(x) =" x2" + bln(x+1),
（1）若对定义域的任意x，都有f(x)≥f(1)成立，求实数b的值；
（2）若函数f(x)在定义域上是单调函数，求实数b的取值范围；
（3）若b = -1,，证明对任意的正整数n，不等式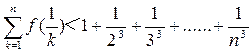都成立
粤公网安备 44130202000953号