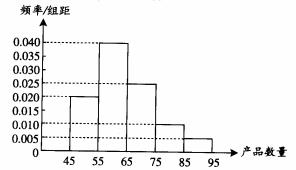
为了调查某厂工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量。产品数量的分组区间为[45,55),[55,65),[65,75),[75,85),[85,95),由此得到频率分布直方图,如右图。
(1)请填完整表格;
(2)估算众数,中位数,平均数。
| 分组 |
45~55 |
55~65 |
65~75 |
75~85 |
85~95 |
| 频数 |
|
|
|
|
|
| 频率 |
|
|
|
|
|
相关知识点
推荐套卷
 出它们的重量(单位:克),重量值落在(495,510]
出它们的重量(单位:克),重量值落在(495,510] 品为合格品,否则为不合格品,表1是甲流水线样本频数分布表,
品为合格品,否则为不合格品,表1是甲流水线样本频数分布表, 图1是乙流水线样
图1是乙流水线样 某食
某食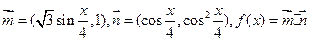 。
。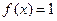 ,求
,求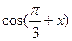 的值;
的值;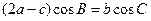 ,
, 的取值范围。
的取值范围。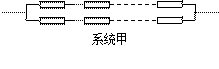
 粤公网安备 44130202000953号
粤公网安备 44130202000953号