(13分)（理科）已知双曲线
与椭圆
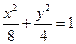有公共焦点，且以抛物线
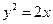的准线为双曲线
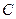的一条准线．动直线
过双曲线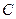的右焦点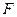
且与双曲线的右支交于
两点．
（1）求双曲线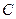的方程；
（2）无论直线绕点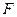怎样转动，在双曲线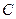上是否总存在定点
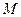，使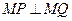
恒成立？若存在，求出点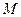的坐标，若不存在，请说明理由．
相关试题
，不等式
的解集是
，
的解析式；
，不等式
恒成立，求t的取值范围．
: 
,
: 
,若
是
的必要不充分条件，求实数
的取值范围.
满足：
，
，
．
及
(
)，求数列
的前n项和
．
的周长为
,且
的长；
,求角C的度数.
的焦点坐标，离心率和渐近线方程.相关知识点
推荐套卷
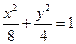(13分)（理科）已知双曲线与椭圆有公共焦点，且以抛物线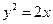的准线为双曲线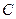的一条准线．动直线过双曲线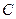的右焦点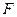且与双曲线的右支交于两点．
（1）求双曲线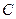的方程；
（2）无论直线绕点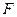怎样转动，在双曲线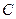上是否总存在定点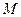，使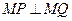恒成立？若存在，求出点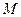的坐标，若不存在，请说明理由．
粤公网安备 44130202000953号