(本小题满分12分)袋子中有质地、大小完全相同的4个球,编号分别为1,2,3,4.甲、乙两人玩一种游戏:甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,若两个编号的和为奇数算甲赢,否则算乙赢.记基本事件为 ,其中
,其中 分别为甲、乙摸到的球的编号。
分别为甲、乙摸到的球的编号。
(1)列举出所有的基本事件,并求甲赢且编号的和为5的事件发生的概率;
(2)比较甲胜的概率与乙胜的概率,并说明这种游戏规则是否公平。(无详细解答过程,不给分)
(3) 如果请你猜这两球的号码之和,猜中有奖.猜什么数获奖的可能性大?说明理由.
推荐套卷
 的定义域为集合A,函数
的定义域为集合A,函数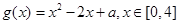 的值域为集合B,若
的值域为集合B,若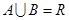 , 求实数
, 求实数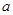 的取值范围.
的取值范围.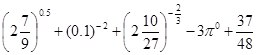
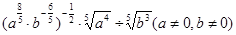
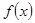 在定义域(0,+∞)上为增函数,且满足
在定义域(0,+∞)上为增函数,且满足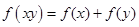 ,
,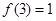 .
.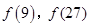 的值;
的值;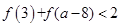 ,求实数
,求实数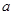 的取值范围.
的取值范围.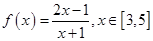 ,
,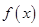 的单调性;
的单调性; 粤公网安备 44130202000953号
粤公网安备 44130202000953号