(本小题13分)
已知函数 的图象在
的图象在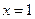 处的切线与直线
处的切线与直线 平行.
平行.
(1)求实数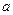 的值;
的值;

(2)若方程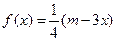 在
在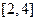 上有两个不相等的实数根,
上有两个不相等的实数根,
求实数 的取值范围;(参考数据:
的取值范围;(参考数据: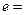 2.71 828…)
2.71 828…)
(3)设常数 ,数列
,数列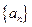 满足
满足 (
( ),
),  ,求证:
,求证: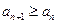 .
.
推荐套卷
(本小题13分)
已知函数 的图象在
的图象在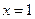 处的切线与直线
处的切线与直线 平行.
平行.
(1)求实数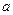 的值;
的值;

(2)若方程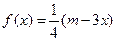 在
在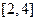 上有两个不相等的实数根,
上有两个不相等的实数根,
求实数 的取值范围;(参考数据:
的取值范围;(参考数据: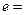 2.71 828…)
2.71 828…)
(3)设常数 ,数列
,数列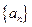 满足
满足 (
( ),
),  ,求证:
,求证: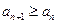 .
.