已知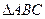 的两个顶点
的两个顶点 的坐标分别
的坐标分别 ,且
,且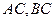 所在直线的斜率之积为
所在直线的斜率之积为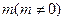 ,1)求顶点
,1)求顶点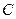 的轨迹.2)当
的轨迹.2)当 时,记顶点
时,记顶点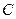 的轨迹为
的轨迹为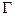 ,过点
,过点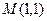 能否存在一条直线
能否存在一条直线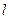 ,使
,使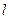 与曲线
与曲线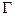 交于
交于 两点,且
两点,且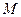 为线段
为线段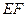 的中点,若存在求直线
的中点,若存在求直线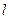 的方程,若不存在说明理由.
的方程,若不存在说明理由.
推荐套卷
已知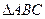 的两个顶点
的两个顶点 的坐标分别
的坐标分别 ,且
,且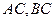 所在直线的斜率之积为
所在直线的斜率之积为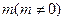 ,1)求顶点
,1)求顶点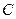 的轨迹.2)当
的轨迹.2)当 时,记顶点
时,记顶点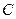 的轨迹为
的轨迹为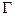 ,过点
,过点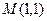 能否存在一条直线
能否存在一条直线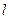 ,使
,使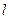 与曲线
与曲线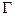 交于
交于 两点,且
两点,且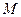 为线段
为线段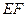 的中点,若存在求直线
的中点,若存在求直线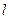 的方程,若不存在说明理由.
的方程,若不存在说明理由.