(本小题满分12分)
(1)连续抛掷两枚正方体的骰子(它们的六个面分别标有数字1,2,3,4,5,6),记所得朝上的面的点数分别为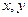 ,过坐标原点和点P(
,过坐标原点和点P(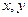 )的直线的倾斜角为
)的直线的倾斜角为  ,求
,求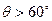 的概率;
的概率;
(2)若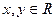 ,且
,且 ,过坐标原点和点P(
,过坐标原点和点P(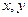 )的直线的斜率为
)的直线的斜率为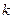 ,求
,求 的概率。
的概率。
推荐套卷
(本小题满分12分)
(1)连续抛掷两枚正方体的骰子(它们的六个面分别标有数字1,2,3,4,5,6),记所得朝上的面的点数分别为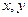 ,过坐标原点和点P(
,过坐标原点和点P(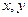 )的直线的倾斜角为
)的直线的倾斜角为  ,求
,求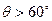 的概率;
的概率;
(2)若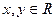 ,且
,且 ,过坐标原点和点P(
,过坐标原点和点P(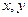 )的直线的斜率为
)的直线的斜率为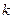 ,求
,求 的概率。
的概率。