(本小题满分12分)
已知椭圆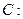
 的离心率为
的离心率为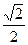 ,点
,点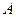 是椭圆上的一点,且点
是椭圆上的一点,且点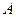 到椭圆
到椭圆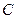 的两焦点的距离之和为4,
的两焦点的距离之和为4,
(1)求椭圆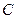 的方程;
的方程;
(2)过点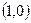 作直线
作直线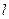 与椭圆
与椭圆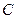 交于
交于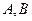 两点,
两点,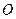 是坐标原点,设
是坐标原点,设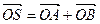 ,是否存在这样的直线
,是否存在这样的直线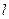 ,使四边形
,使四边形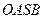 的对角线长相等?若存在,求出
的对角线长相等?若存在,求出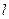 的方程,若不存在,说明理由。
的方程,若不存在,说明理由。
推荐套卷
(本小题满分12分)
已知椭圆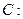
 的离心率为
的离心率为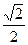 ,点
,点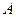 是椭圆上的一点,且点
是椭圆上的一点,且点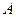 到椭圆
到椭圆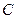 的两焦点的距离之和为4,
的两焦点的距离之和为4,
(1)求椭圆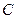 的方程;
的方程;
(2)过点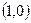 作直线
作直线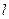 与椭圆
与椭圆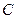 交于
交于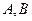 两点,
两点,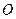 是坐标原点,设
是坐标原点,设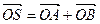 ,是否存在这样的直线
,是否存在这样的直线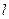 ,使四边形
,使四边形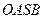 的对角线长相等?若存在,求出
的对角线长相等?若存在,求出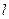 的方程,若不存在,说明理由。
的方程,若不存在,说明理由。