(本小题满分12分)
已知函数 ,
,
(1) 若 ,
, ,且
,且 的定义域是[– 1,1],P(x1,y1),Q(x2,y2)是其图象上任意两点(
的定义域是[– 1,1],P(x1,y1),Q(x2,y2)是其图象上任意两点(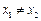 ),设直线PQ的斜率为k,求证:
),设直线PQ的斜率为k,求证: ;
;
(2) 若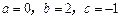 ,且
,且 的定义域是
的定义域是 ,
,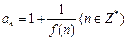 .
.
求证: .
.
推荐套卷
(本小题满分12分)
已知函数 ,
,
(1) 若 ,
, ,且
,且 的定义域是[– 1,1],P(x1,y1),Q(x2,y2)是其图象上任意两点(
的定义域是[– 1,1],P(x1,y1),Q(x2,y2)是其图象上任意两点(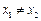 ),设直线PQ的斜率为k,求证:
),设直线PQ的斜率为k,求证: ;
;
(2) 若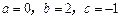 ,且
,且 的定义域是
的定义域是 ,
,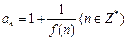 .
.
求证: .
.