(本小题12分) 已知二次函数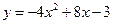 。
。
(1)指出图像的开口方向、对称轴方程、顶点坐标;
(2)画出它的图像,并说明其图像由 的图像经过怎样平移得来;
的图像经过怎样平移得来;
(3 )求函数的最大值或最小值;
)求函数的最大值或最小值;
(4)写出函数的单调区间(不必证明)。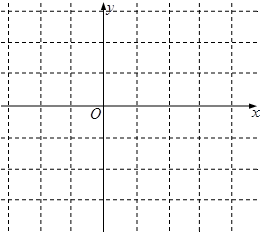
相关知识点
推荐套卷
(本小题12分) 已知二次函数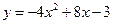 。
。
(1)指出图像的开口方向、对称轴方程、顶点坐标;
(2)画出它的图像,并说明其图像由 的图像经过怎样平移得来;
的图像经过怎样平移得来;
(3 )求函数的最大值或最小值;
)求函数的最大值或最小值;
(4)写出函数的单调区间(不必证明)。